论文题目：DEST-GNN: A double-explored spatio-temporal graph neural network for multi-site intra-hour PV power forecasting

发表时间：2025 Applied Energy (影响因子：10.1)

论文作者：Yanru Yang, Yu Liu, Yihang Zhang, Shaolong Shu, Junsheng Zheng

作者单位：同级大学

1. 背景

1.1 介绍

目前，已经开发了各种可再生能源以应对由传统化石燃料引起的环境污染和能源短缺的挑战。在这些可再生能源中，光伏技术在产生清洁和可持续能源方面受到高度重视。然而，光伏发电的特点是其固有的波动性和间歇性，这受到不可预测和不断变化的天气模式的影响，因此光伏系统集成到电网中具有一定的难度。光伏发电功率预测是为了提高光伏并网电网的稳定性和安全性而发展起来的。它在平衡电网、优化存储系统、确保自动发电控制和维持运行调节储备方面非常重要。

到目前为止，光伏发电预测已经得到了广泛的研究。根据预测时间范围，可分为小时内（0-1小时）、日内（0-24小时）和日前（24-48小时）预测。本文主要研究了传感器时间序列数据的小时内功率预测问题，这对于在实时调度、维护计划和电网市场运营等方面有效地管理电网至关重要。

一般来说，光伏发电的预测模型大致分为物理的和数据驱动的方法。物理方法采用理论模拟模型计算输出功率。因此，对于在设计文档中具有可用的所有必要信息的光伏电站所有者，这些方法在功率预测中表现良好。数据驱动的方法在很大程度上依赖于历史功率数据或其他与辐照度相关的数据，并且它们不需要关于PV系统的设计参数的任何信息。

在现实中，多个光伏电站密集分布在一个区域内，可以视为密集网络。当我们预测一个光伏电站的功率时，我们可以使用它的邻居的信息来提高预测性能。因此，多站点小时内光伏功率预测变得有意义。通过考虑PV站之间的空间和时间关系，可以有效地捕获云覆盖和移动，因为经过的云对相邻的PV站有顺序的影响。

1.2 目前存在的问题

近年来，在多站点光伏发电小时内预测方面取得了一些进展，但仍存在以下两个关键问题。

1、将邻近地点的空间光伏功率信息作为输入变量，可大大提高预测的准确性。但是，分配给这些相关站点的权重，反映了它们的相关性，往往依赖于经验，因此无法捕捉到隐藏在采样数据中的所有信息。

2、由于风速和风向的变化、云的移动和其他因素，这些相关地点之间的权重应是时变的。但预定义的权值是随时间不变的，因此不能全面地提取多个PV序列在空间和时间维度上的动态特征。

1.3 本文贡献

本文提出了一个双重探索的时空图神经网络（DEST-GNN）用于多个站点的小时内光伏功率预测。

1、提出了一种新的DEST-GNN多站小时内光伏发电功率预测方法，该方法充分利用了多个发电站之间复杂的时空关系，通过集成代表这些站点之间的校正信息的权重矩阵Ea和代表这些站点之间的校正动态变化的调整矩阵S来实现。然后将自适应学习邻接矩阵输入到GCN中，以提取各个光伏电站之间的复杂时空模式。

2、权值矩阵的确定不是基于经验，而是通过从样本中学习而获得的。该学习过程在GCN的训练过程中完成，以达到最佳性能。

3、通过提取模型输入之间复杂的时空相关性，得到准确反映当前动态变化的调整矩阵S。特别地，采用稀疏时空关注度对时空相关性进行加权，在充分利用动态关系的同时，消除了电站间的低相关性。

2. 问题表述

在这项研究中，目标是使用过去P时间步长的光伏发电数据预测多个站点的光伏发电在未来M时间步长的发电数据。对N个发电站数据，有x_0=[x_0^1,x_0^2,...,x_0^N]表示当前发电数据。

过去P时间步长的发电数据表示为：x_{-p+1},x_{-p+2},...,x_0，并且未来M时间步长的发电数据表示为：x_1,x_2,...,x_M。

使用无向图G=(V,E,A)来表示N个光伏电站之间的相关性。在图中，V是N个光伏电站节点的集合。E是表示两个节点关系的边。使用邻接矩阵A表示所有站点之间的关系。

功率预测任务是找到从PV功率的过去时间步长数据到未来时间步长数据的映射f(·)：[x_{-p+1},x_{-p+2},...,x_0;G] \overset{f(·)}{\rightarrow}x_1,...,x_M

3. 整体结构

为预测N个光伏电站的光伏发电功率，本文提出了DEST-GNN来拟合f(·)。所提出的DEST-GNN模型的结构，旨在探索N个电站时间电力数据 空间和时间的相关性。整体结构如下图：

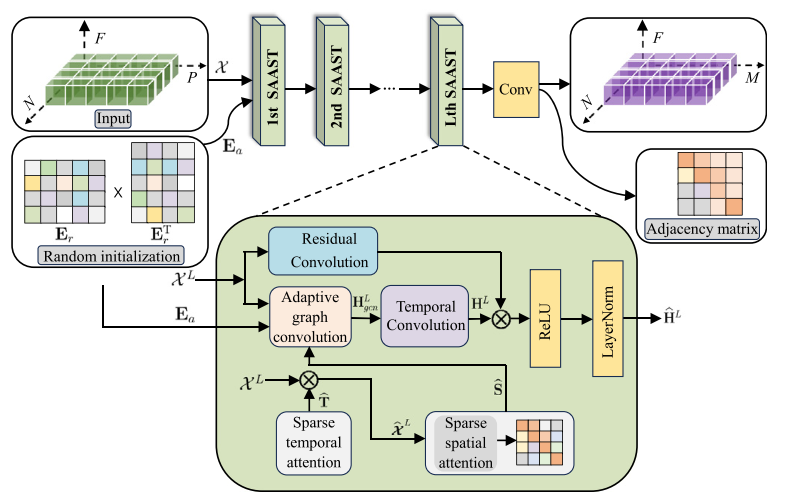
它是由几个基于系数注意力的自适应时空块（SAAST）和一个输出层连接组成的。

对SAAST，使用稀疏注意力而不是传统的注意力，以减轻输入数据的低相关性和噪声的负面影响。稀疏时空注意模块的输出送入时空卷积模块，首先进行自适应谱卷积的GCN融合相邻电站的空间相关性信息，然后应用TCN融合时间关系。随后，时间卷积模块的输出进入输出层，以获得最终的多站点光伏功率预测结果。

3.1 稀疏注意力

在光伏发电时间序列数据中，不同历史数据对预期预测的重要性可能不同。稀疏注意机制允许模型集中于与预测强烈相关的信息点，从而在减少计算量的同时消除冗余信息。因此，本文利用同时关注空间和时间方面的稀疏注意机制来有效地捕获时空相关性。

3.1.1 稀疏时间注意

PV功率数据的时间相关性表示为周期性时间序列，随不同的时间间隔而变化。注意力机制使模型能够集中于输入序列的某些特定时间步长，从而提高了模型的性能。然而，传统的注意力机制依赖于所有时间点都相关的假设，这可能引入无效的相关性。因此，本文使用稀疏注意技术来捕捉各个时间点的时间相关性，同时减轻低相关性和噪声的负面影响。传统的时间注意力可以描述为：

其中T是时间相关矩阵，表示之前时间步长之间的相关性。时间注意力的输入为x^L=x_1,x_2,...,x_p\in\mathbb{R}^{N×F×P}。F的值为1代表幂特征的一个维度。\sigma是sigmoid激活函数V_t,b_t\in\mathbb{R}^{P\times P},W_1\in\mathbb{R}^N,W_2\in\mathbb{R}^{F\times N},W_3\in\mathbb{R}^F是可学习的参数。

为了使该过程更有效，稀疏操作可以消除对预测输出具有低影响或没有影响的时间点。稀疏时间机制被描述为：

其中，\hat{T}_{i,j}是时间步i和j的标准化相关值；\tau是相关性的阈值，本文使用平均值\bar{T_{i,j}}作为阈值，以证明整体时间相关性的大小。

然后使用\hat{T}来调整输入x^L：\hat{x}^L=x^L\otimes\hat{T}，其中\hat{x}^L是组合的动态时间关系输出。运算为hadamard积。

3.1.2 稀疏空间注意

从多个光伏电站采集的时间序列数据具有固有的空间特征。天气变化和云移动会对光伏电站功率产生影响。换句话说，考虑某个区域内的光伏板的功率，从而也间接地考虑了天气的影响，可以提高功率预测的准确性。为此，在稀疏时间注意的基础上，采用稀疏空间注意来评估空间相关性，消除噪声和多站点光伏发电系统间弱相关性的影响。稀疏空间注意的目标是基于\hat{x}^L 来训练一个N×N的矩阵，类似于上节中的稀疏时间注意。传统的空间注意表示为：

其中，S是空间相关性矩阵；\hat{x}^L 是稀疏时间注意力的输出；V_t,b_t\in\mathbb{R}^{N\times N},W_1\in\mathbb{R}^P,W_2\in\mathbb{R}^{F\times P},W_3\in\mathbb{R}^F 是可学习的参数。本文使用softmax来规范化对称空间注意力，并设计稀疏空间注意力如下：

设置同上小节时间注意力设置，使用平均值作为阈值。

3.2 自适应图卷积网络

图卷积网络可以用图结构数据捕获空间特征。然而，静态邻接矩阵不能准确地表示站点之间随时间变化的关系。因此，提出了自适应邻接矩阵来学习站之间的复杂相关性。因此，自适应GCN用于学习基于图结构的节点表示。谱GCN是指对图结构数据的卷积运算。

对给定的图G，节点信号x通过核g_\theta过滤：g_\theta * x =g_\theta(L)x = g_\theta(U\Lambda U)x。

图的标准拉普拉斯矩阵L定义：L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U\Lambda U^T，其中I_N是单位矩阵；D是度矩阵且D_{ii}=\sum_jA_{ij}；A是邻接矩阵，用以提供图的结构信息；U是一个正交矩阵；\Lambda是由L的特征值构成的对角矩阵。

然后，利用K阶切比雪夫多项式来进行图卷积运算：g_\theta * x =\sum_{k=0}^{K-1}\theta_kT_k(\tilde{L})x，其中\theta_k \in \mathbb{R}^K是切比雪夫系数向量。切比雪夫多项式的递归定义是：T_k=2xT_{k-1}(x)-T_{k-2}(x),T_0(x)=1 且T_1(x)=x；\tilde{L}=\frac{2}{\lambda_{max}}L-I_N，\lambda_{max}是L的最大特征值。

上述卷积是基于预定义的图结构。然而，不同发电站之间的潜在时空相关性没有明确的预定义的图形，并且经验定义的图形不能充分反映真实的场景中的时空相关性。因此，我们利用可学习的邻接矩阵Ea来构造图结构，取代传统的拉普拉斯矩阵：E_a=softmax(\delta( E_r \cdot E_r^T))，Er是可学习的矩阵，被随机初始化，然后通过训练优化；d为矩阵维数。利用softmax对自适应矩阵进行归一化处理；\delta是ReLU激活函数。

对自适应邻居矩阵Ea的图卷积过程可以描述如下：

因此，该表示不仅包含距离或相关性，还可以包含内在信息。所提出的自适应图卷积表述为：

其中，H_{gcn}^L是第L个SAAST块中自适应GCN的输出；\hat{S}是稀疏空间注意模块的输出。归一化稀疏关注度的权值分配影响特征的表示，归一化稀疏关注度反映了多站点间的动态空间关系。因此，自适应GCN能有效捕获多站点内在联系，提高模型性能。

3.3 时间卷积网络

一旦自适应图卷积操作已经从空间维度中的相邻节点收集了信息，时间卷积层将通过组合来自历史时间片的信息来更新每个节点的信号。时间卷积过程可以表示为：H_L=T_{conv}*H_{gcn}^L，H^L 是第L个SAAST块的时间卷积子模块输出；Tconv表示时间卷积运算。

然后利用一个残差模块Rconv来处理x^L ，对第L个SAAST块的时间卷积结果和残差卷积结构进行矩阵加法：

\hat{H^L} 是第L个SAAST块的输出。

残差模块的加入有效地解决了与深度网络中训练困难和梯度消失相关的挑战，从而提高了模型性能。

3.4 光伏预测框架

如图所示为方法的实现过程：

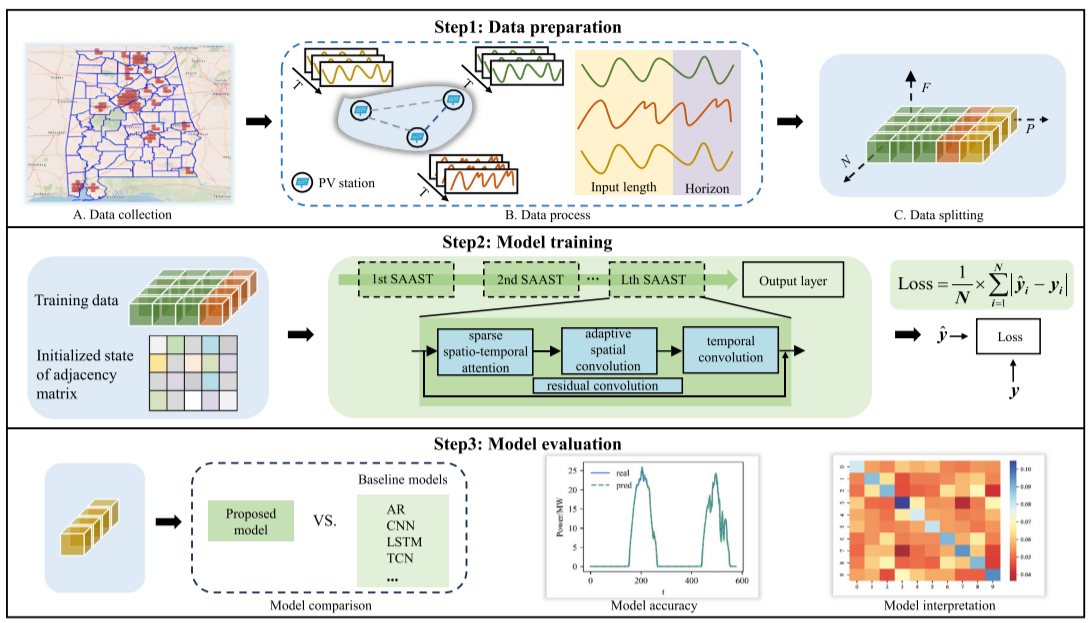
首先，数据准备包括数据收集、数据处理和数据拆分。数据处理包括处理缺失值和离群值。本文中用于评估所提出的方法的数据分为三部分：60%用于训练，20%用于验证，20%用于测试。然后使用计算的均值和方差对训练集执行标准归一化操作。

第二步是模型训练。在这一步中，提出的DESTGNN由多个块堆叠和一个输出层组成。每个SAAST块包含稀疏时空注意、自适应空间卷积、时间卷积和残差卷积。前一个SAAST块的输出是下一个SAAST块的输入。训练集作为DEST-GNN的输入用于模型训练，而验证集用于选择模型参数。在训练过程中使用平均绝对误差（MAE）损失。

最后一步是模型评估。在测试集数据上测试训练的模型，并基于误差度量评估模型。此外，还与基线进行了比较。我们还对实验结果进行了综合分析。

4. 实验以及分析

4.1 数据集

在本研究中，我们利用阿拉巴马州和加利福尼亚州的数据集进行案例研究。这些数据集是国家可再生能源实验室(NREL)创建的全国数据集的一部分。它们是使用亚小时辐照度算法生成的，2006年全年的分辨率为5分钟。http://www.nrel.gov/grid/solar-power-data.html。在数据集中，电站分为两类:单轴跟踪的公用事业规模PV和固定倾斜等于纬度的分布式PV。

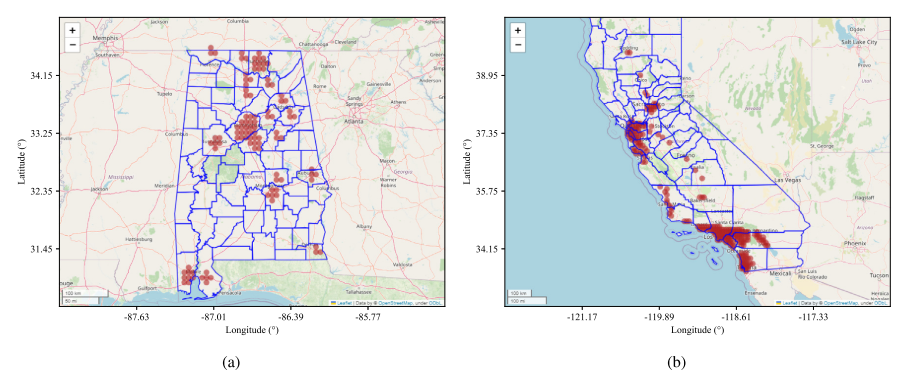(a)阿拉巴马州数据集中103个分布式PV系统的位置。(b)加利福尼亚州数据集上238个分布式PV系统的位置。

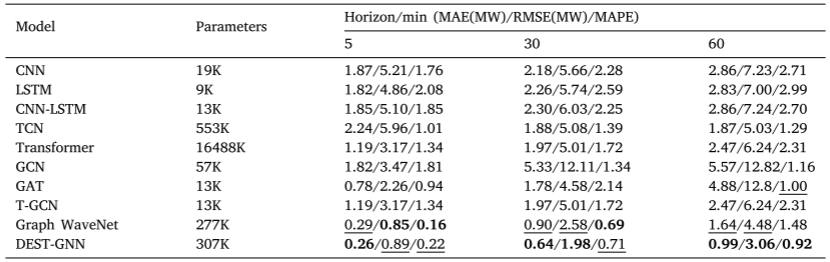
4.2 结果

评估指标包括MAE、均方根误差(RMSE)和平均绝对百分比误差(MAPE)。

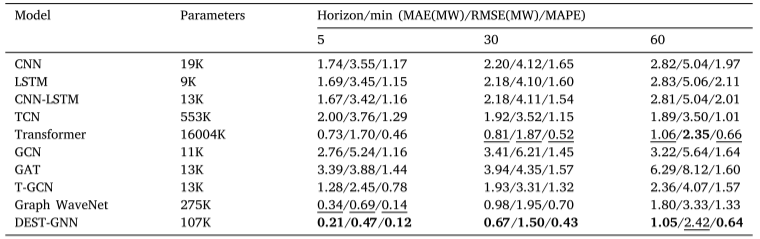
5. 结论

本文提出了一种新的多站点小时内PV功率预测模型——DEST-GNN。它主要包含SAAST块。每个SAAST包括稀疏注意、自适应谱图卷积、时间卷积和残差模块。稀疏注意有效地识别了无效相关性，增强了捕捉电力数据时空模式的能力。通过可学习的自适应邻接矩阵，该模型从电力数据中学习内部空间依赖关系，从而消除了对预定义图形信息的需求。通过结合自适应谱图卷积和时间卷积，该模型有效地捕获了时空特征。双重探索的时空能力使我们提出的方法适用于多站点间的时间序列数据建模。此外，残差模块的集成保证了网络性能的鲁棒性和可靠性。

未来，未来工作的重点将是在保持模型低复杂度的同时进一步提高模型的准确性。这涉及探索先进的优化技术，创新的架构修改，以及更有效的特征提取方法，这些方法可以在不显着增加模型复杂性的情况下提高性能。

========================================================================

总结：

创新点：

1.同时预测每个光伏电站的功率，同时考虑与其他电站的时空相关性。

2.通过稀疏注意力机制，模型能够过滤掉电站之间的弱关联，提高预测精度。

可改进之处：

1.数据处理过程比较简单

2.