DJ的小网站

Menu

cdj
Published on 2024-11-03 / 68 Visits
0

论文汇报0：Retentive Network: A Successor to Transformer for Large Language Models

#Transformer#大语言模型

论文题目：Retentive Network: A Successor to Transformer for Large Language Models

发表时间：2023 arxiv

论文作者：Yutao Sun, Li Dong, Shaohan Huang, Shuming Ma, Yuqing Xia, Jilong Xue, Jianyong Wang, Furu Wei

作者单位：微软亚洲研究院， 清华大学

1. 背景

1.1 介绍

Transformer是目前大语言模型的基础架构，最初提出的时候是为了解决模型顺序训练的问题。相较于RNN模型，Transformer模型解决了以下问题：

  1. 长序列依赖问题

RNN模型的输入是序列，只能按照顺序处理数据，并且因为存在梯度爆炸/消失的问题，无法捕捉到长序列的依赖关系。Transformer通过引入自注意力机制，考虑所有位置的信息，解决了长序列问题。

  1. 无法并行计算

传统的RNN模型需要按照顺序处理序列中的元素，无法进行并行计算。Transformer的自注意力和多头注意力可以并行计算，大大提高了训练和推理的效率。

  1. 训练效率低

RNN往往需要更多的训练步骤才能到达局部/全局最优。深层的RNN具有许多参数，并且这些参数大部分是相互关联的。

然而Transformer的训练并行性是以低效的推理为代价的，其每一步推理的的复杂度是O（N）的，不断增长的序列长度增加了GPU内存消耗和延迟，并降低了推理速度。因此，为了实现保留训练的并行性和有竞争力的性能，开发出了许多新的模型，但是实现上述目标存在不可能三角，即不能同时达成训练并行性，良好的性能与低推理成本。

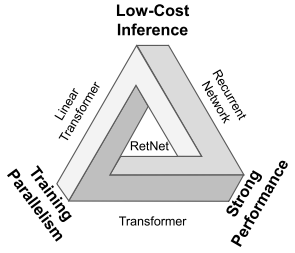
不可能三角

目前主要有三个研究方向：

  1. Linear Transformer：主要处理方式是对k和v进行处理，但是此方法的建模能力和性能不如Transformer。

  2. Recurrent Network：随着不断的优化，最大的缺点就是不能并行训练。

  3. 用其他机制替换注意力。

1.2 研究结果

提出了Retentive Network，同时实现了低成本推理，高效的长序列建模以及可媲美Transformer的性能和并行模型训练。引入了多尺度保留机制来替代多头注意力，该机制有三种范式：并行——使训练并行性能够充分利用GPU设备；循环——在内存和计算方面实现了高效的O(1)推理，显著降低部署成本和延迟；块循环表征——实现高效的长序列建模。通过并行编码每个局部块提高计算速度，同时循环编码全局块节省GPU内存。模型性能如下：

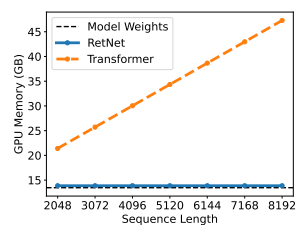
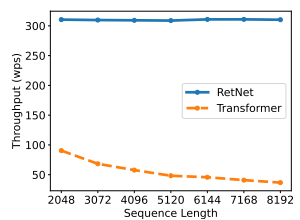
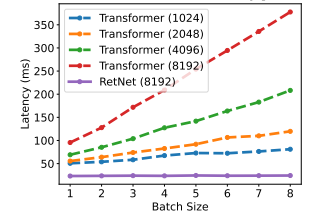
2 方法-Retentive Networks

先导：一文通透位置编码：从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA 2 Long(含NTK-aware简介)

RetNet架构和Transformer类似，也是堆叠L层同样的模块，每个模块内部包含两个子模块：一个multi-scale retention（MSR）和一个 feed-forward network (FFN)。

2.1 retention

首先给定一个输入序列{\{x_i\}}^{|x|}_{i-1}: x=x_1…x_{|x|}其中|x|代表序列的长度，经过Embedding得到词嵌入向量X^0。

对给定输入词嵌入序列X \in \mathbb{R}^{|x|×d}中每个时间步n的向量X_n \in \mathbb{R}^{1×d} 都乘以权重值w_v \in \mathbb{R}^{d×d}得到v_n \in \mathbb{R}^{1×d}：v_n = X_n ·w_v

然后有类似Transformer架构的Q和K的投影：Q=XW_Q,K=XW_K

其中W_Q,W_K \in \mathbb{R}^{d×d}是需要学习的权值。

假设现在有一个序列建模的问题，通过S_n \in \mathbb{R}^{d×d}将v_n映射为o_n向量：

s_n = As_{n-1}+K_n^{T}v_n\\ o_n=Q_ns_n=\sum_{m=1}^nQ_nA^{n-m}K_m^Tv_m

其中A \in \mathbb{R}^{d×d}是一个矩阵。

上面Q_ns_n展开：

\begin{aligned} Q_ns_n &=Q_n(As_{n-1}+K_n^Tv_n) \\ & =Q_n(A(As_{n-2}+K_{n-1}^Tv_n-1)+K_n^Tv_n)\\ & =Q_n(A^2s_{n-2}+A^1K_{n-1}^T+A^0K_n^Tv_n) \\ & …… \end{aligned}

对矩阵A，定义A为一个可对角化的矩阵：

A=\Lambda(\gamma e^{i\theta})\Lambda^{-1}

其中\gamma,\theta \in \mathbb{R}^d都是d维的向量，\Lambda是一个可逆矩阵，通过欧拉公式e^{ix}=cosx+i sinx，\gamma e^{i\theta}就是一个对角矩阵，对角元素的值就对应将\gamma和e^{i\theta}转成负数向量相乘再将结果转回实数向量的结果。

因此可以得到A^{n-m}=\Lambda(\gamma e^{i\theta})^{n-m}\Lambda^{-1}，再将\Lambda吸收进W_Q和W_K，也就是W_Q\Lambda和\Lambda^{-1}W_K^T，分别用W_Q和W_K^T替代，当作学习的权重，最后将\gamma修改为一个实数常量，最终得到o_n的计算公式：

\begin{aligned} o_n&=\sum_{m=1}^nQ_n(\gamma e^{i\theta})^{n-m}K_m^Tv_m \\ &=\sum_{m=1}^n Q_n(\Lambda(\gamma e^{i\theta})^{n-m}\Lambda^{-1})K_m^Tv_m \\ &=\sum_{m=1}^nX_nW_Q\Lambda(\gamma e^{i\theta})^{n-m}\Lambda^{-1}(X_mW_K)^Tv_m \\ &= \sum_{m=1}^n(Q_n(\gamma e^{i\theta})^n)(K_m(\gamma e^{i\theta})^{-m})^Tv_m \\ &=\sum_{m=1}^n\gamma^{n-m}(Q_ne^{in\theta})^n)(K_m(e^{i(-m)\theta})^{-m})^Tv_m \end{aligned}

借助欧拉公式，e^{i(-m)\theta}=[cosm\theta_1,-sinm\theta_2,...,cosm\theta_{d-1},-sinm\theta_d]，转为复数形式就是：e^{i(-m)\theta}=[cosm\theta_1-sinm\theta_2,...,cosm\theta_{d-1}-sinm\theta_d] ，刚好对应e^{im\theta}的共轭：e^{im\theta}=[cosm\theta_1+sinm\theta_2,...,cosm\theta_{d-1}+sinm\theta_d]，所以可得o_n=\sum_{m=1}^n\gamma^{n-m}(Q_ne^{in\theta})(K_me^{im\theta})^\dagger v_m。Q_ne^{in\theta}和K_me^{im\theta}就是对Q_n和K_m应用旋转式位置编码。其思想是采用绝对位置编码的形式实现相对位置编码

一、 并行训练表示

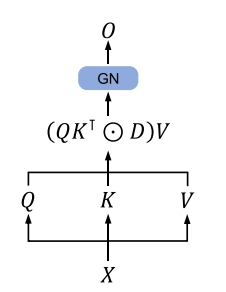
如上图为Retention层的并行表示，GN表示GroupNorm，其公式定义如下：

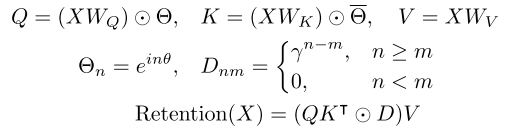
\bar\Theta对应\Theta矩阵的共轭，D是一个下三角矩阵，通过这个矩阵可以根据距离削弱关系，在n＜m中出现0表示一个自回归关系，也就是只能注意到前面的内容，达到如下图的结果：

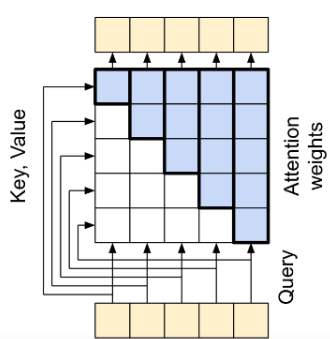
对应的代码实现如下：

def forward(self, X):

        sequence_length = X.shape[1]
        # 计算D矩阵，权重
        D = self._get_D(sequence_length).to(self.W_Q.device)

        Q = (X @ self.W_Q)
        K = (X @ self.W_K)
        # 应用xpos方法，获得旋转式坐标编码
        Q = self.xpos(Q)
        K = self.xpos(K, downscale=True)
        V = X @ self.W_V
        # 计算注意力得分，通过Q和K的转置矩阵相乘，然后乘以D进行缩放
        ret = (Q @ K.permute(0, 2, 1)) * D.unsqueeze(0)
        return ret @ V

二、 循环推理表示

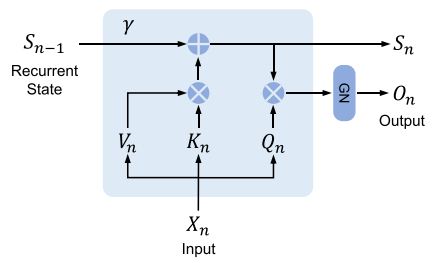
如上图为Retention层的循环表示，其公式定义如下：

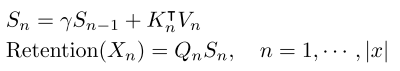
可以看到在推理阶段，RetNet在计算当前时间步n的输出O_n只依赖上一个时间步输出的状态矩阵S_{n-1}。

与Transformer在每个时间步的计算要先算Q_n和前面所有时间步的K相乘得到attention权值再和V相乘求和相比，就是将计算顺序改了一下，先计算了K_n和V_n的相乘，并一直累加到状态矩阵S_n上，最后再和Q_n相乘。

def forward_recurrent(self, x_n, s_n_1, n):
        Q = (x_n @ self.W_Q)
        K = (x_n @ self.W_K)

        Q = self.xpos(Q, n+1)
        K = self.xpos(K, n+1, downscale=True
        V = x_n @ self.W_V
        # 计算当前时间步的状态s_n，它是上一个时间步的状态s_n_1和当前时间步的K与V的注意力加权和
        # K: (batch_size, 1, hidden_size)
        # V: (batch_size, 1, v_dim)
        # s_n = gamma * s_n_1 + K^T @ V
        s_n = self.gamma * s_n_1 + (K.transpose(-1, -2) @ V)
        # 返回当前时间步的Q与s_n的乘积以及更新后的状态s_n
        return (Q @ s_n), s_n

三、记忆的组块循环表示

并行表示和循环表示的混合形式可用于加速训练，特别是对长序列。将输入分成多个块，在块内遵循并行表示进行计算，而在块间按照循环表示传递，第i个块的Retention输出为：

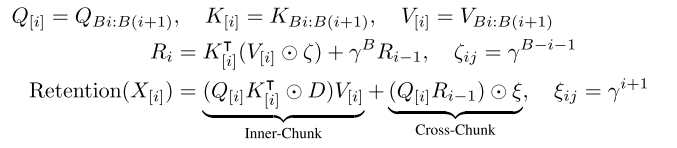
B表示第i块的长度。

def forward_chunkwise(self, x_i, r_i_1, i):
        """
        Chunkwise representation of the retention mechanism.
        x_i: (batch_size, chunk_size, hidden_size)
        r_i_1: (batch_size, hidden_size, v_dim)
        """
        batch, chunk_size, _ = x_i.shape
        D = self._get_D(chunk_size)

        Q = (x_i @ self.W_Q)
        K = (x_i @ self.W_K)

        Q = self.xpos(Q, i * chunk_size)
        K = self.xpos(K, i * chunk_size, downscale=True)
        V = x_i @ self.W_V
        # 计算当前块的状态r_i
        r_i =(K.transpose(-1, -2) @ (V * D[-1].view(1, chunk_size, 1))) + (self.gamma ** chunk_size) * r_i_1
        # 计算当前块内的注意力输出
        inner_chunk = ((Q @ K.transpose(-1, -2)) * D.unsqueeze(0)) @ V
        
        # 计算跨块注意力权重
        #e[i,j] = gamma ** (i+1)
        e = torch.zeros(batch, chunk_size, 1)
        for _i in range(chunk_size):
            e[:, _i, :] = self.gamma ** (_i + 1)
        # 计算跨块的注意力输出
        cross_chunk = (Q @ r_i_1) * e
        # 返回当前块内的注意力输出和跨块的注意力输出的和，以及更新后的状态r_i
        return inner_chunk + cross_chunk, r_i

2.2 多尺度保留Gated Multi-Scale Retention

Gated Multi-Scale Retention，MSR 多尺度保留机制类似多头注意力机制，模型的维度d_{model}，每个头的维度为d，共有d_{model}/d个头，每个头和多头注意力一样使用不同的W_Q,W_K,W_V，同时每个头采用不同的\gamma常量。

对输入X，MSR层的输出为：

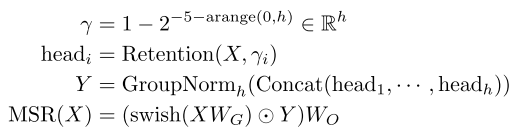
又因为每个头采用了不同的\gamma常量，所以每个头的输出需要单独做normalization，这里利用GroupNorm的尺度不变性来提高保留层的数值精度，在GroupNorm内乘以标量值不影响输出和反向梯度。

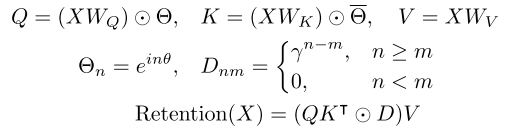
GroupNorm(\alpha*head_i)=GroupNorm(head_i)

将上面式子中的QK_T换成QK_T/\sqrt{d};D_{nm}换成D_{nm}/\sqrt{\sum_{i=1}^nD_{ni}};R_{nm}换成R_{nm}/max(|\sum_{i=1}^nR_{ni}|,1);由于尺度不变性，这些修改不影响最终结果，同时稳定了正向和反向过程的数据。

def forward_chunkwise(self, x_i, r_i_1, i):
        """
        Chunkwise representation of the retention mechanism.
        x_i: (batch_size, chunk_size, hidden_size)
        r_i_1: (batch_size, hidden_size, v_dim)
        """
        batch, chunk_size, _ = x_i.shape
        D = self._get_D(chunk_size)

        Q = (x_i @ self.W_Q)
        K = (x_i @ self.W_K)

        Q = self.xpos(Q, i * chunk_size)
        K = self.xpos(K, i * chunk_size, downscale=True)
        V = x_i @ self.W_V
        
        r_i =(K.transpose(-1, -2) @ (V * D[-1].view(1, chunk_size, 1))) + (self.gamma ** chunk_size) * r_i_1

        inner_chunk = ((Q @ K.transpose(-1, -2)) * D.unsqueeze(0)) @ V
        
        #e[i,j] = gamma ** (i+1)
        e = torch.zeros(batch, chunk_size, 1)
        
        for _i in range(chunk_size):
            e[:, _i, :] = self.gamma ** (_i + 1)
        
        cross_chunk = (Q @ r_i_1) * e
        return inner_chunk + cross_chunk, r_i

2.3 Retention网络的总体结构

对L层Retention网络，通过堆叠MSR和FFN来构建模型，最终过程表示如下：

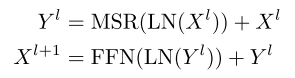
LN为层标准化，FFN(X)=gelu(XW_1)W_2，W_1,W_2是参数矩阵。

类似于Transformer的红框部分，最主要的区别就是把MHA换成MSR：

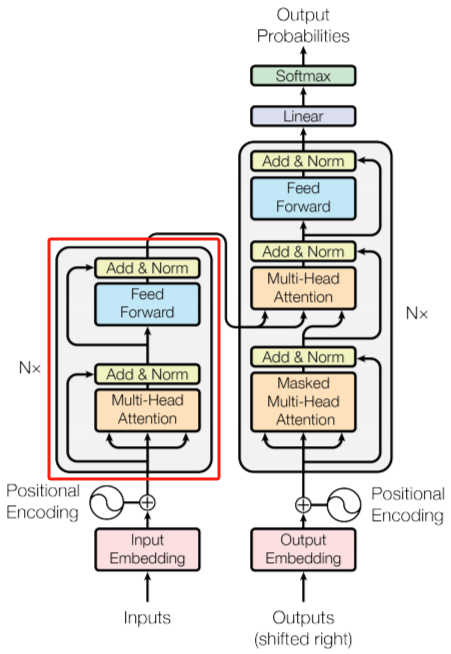
整体代码如下：

class MultiScaleRetention(nn.Module):
    def __init__(self, hidden_size, heads, double_v_dim=False):
        super(MultiScaleRetention, self).__init__()
        self.hidden_size = hidden_size
        self.v_dim = hidden_size * 2 if double_v_dim else hidden_size
        self.heads = heads
        assert hidden_size % heads == 0, "hidden_size must be divisible by heads"
        self.head_size = hidden_size // heads
        self.head_v_dim = hidden_size * 2 if double_v_dim else hidden_size
        # 为每个头计算指数衰减的gamma值
        self.gammas = (1 - torch.exp(torch.linspace(math.log(1/32), math.log(1/512), heads))).detach().cpu().tolist()

        self.swish = lambda x: x * torch.sigmoid(x)
        # 定义输入和输出线性变换的可学习参数
        self.W_G = nn.Parameter(torch.randn(hidden_size, self.v_dim) / hidden_size)
        self.W_O = nn.Parameter(torch.randn(self.v_dim, hidden_size) / hidden_size)
        self.group_norm = nn.GroupNorm(heads, self.v_dim)
        # 创建一个SimpleRetention模块列表，每个gamma值对应一个
        self.retentions = nn.ModuleList([
            SimpleRetention(self.hidden_size, gamma, self.head_size, double_v_dim) for gamma in self.gammas
        ])

    def forward(self, X):
         # 对X应用每个单独的retention机制并收集结果
        Y = []
        for i in range(self.heads):
            Y.append(self.retentions[i](X))
        
        Y = torch.cat(Y, dim=2)
        Y_shape = Y.shape
        Y = self.group_norm(Y.reshape(-1, self.v_dim)).reshape(Y_shape)

        return (self.swish(X @ self.W_G) * Y) @ self.W_O
    
    def forward_recurrent(self, x_n, s_n_1s, n):    
        # 对X的一个切片应用每个单独的retention机制并收集结果和状态
        Y = []
        s_ns = []
        for i in range(self.heads):
            y, s_n = self.retentions[i].forward_recurrent(
                x_n[:, :, :], s_n_1s[i], n
                )
            Y.append(y)
            s_ns.append(s_n)
        
        Y = torch.cat(Y, dim=2)
        Y_shape = Y.shape
        Y = self.group_norm(Y.reshape(-1, self.v_dim)).reshape(Y_shape)
        
        return (self.swish(x_n @ self.W_G) * Y) @ self.W_O, s_ns

    def forward_chunkwise(self, x_i, r_i_1s, i):
        batch, chunk_size, _ = x_i.shape

        # 对X的一个切片应用每个单独的retention机制并收集结果和状态
        Y = []
        r_is = []
        for j in range(self.heads):
            y, r_i = self.retentions[j].forward_chunkwise(
                x_i[:, :, :], r_i_1s[j], i
                )
            Y.append(y)
            r_is.append(r_i)
        
        
        Y = torch.cat(Y, dim=2)
        Y_shape = Y.shape
        Y = self.group_norm(Y.reshape(-1, self.v_dim)).reshape(Y_shape)

        return (self.swish(x_i @ self.W_G) * Y) @ self.W_O, r_is

总结

简单来说，retnet = linear attention + RoPE（旋转式位置编码） + 显式衰减（即 γ），相较于RWKV有进步，简化了模型设计。但是，显示衰减也是RNN被诟病的原因，因为对于长序列，RNN必然不能有效地获得全局依赖，同时也意味着它会对prompt的形式比较敏感。

"prompt" 是指向模型提供输入以引导其生成特定输出的文本或指令。它是与模型进行交互时用户提供的文本段落，用于描述用户想要从模型获取的信息、回答、文本等内容。Prompt 的目的是引导模型产生所需的回应，以便更好地控制生成的输出。

对于语言模型，prompt 可以是一个简短的问题、一个完整的段落，或者是一组指令，这取决于用户的需求和场景。在生成文本时，模型会试图理解 prompt 并根据其理解生成相应的响应。这就是为什么 prompt 很重要，因为它直接影响着模型生成的文本的内容、风格和质量。

论文汇报1：RMT: Retent...

Comment