DJ的小网站

Menu

cdj
Published on 2024-11-04 / 17 Visits
0

论文汇报1：RMT: Retentive Networks Meet Vision Transformers

#Transformer#目标检测

论文题目：RMT: Retentive Networks Meet Vision Transformers

发表时间：2024 CVPR

论文作者：Qihang Fan, Huaibo Huang, Mingrui Chen, Hongmin Liu, Ran He

作者单位：中国科学院自动化研究所，中国科学院大学，北京科技大学

1.背景

1.1 介绍

近年来，Vision Transformer(ViT)在计算机视觉领域得到了越来越多的关注，然而ViT的核心部分Self-Attention缺乏明确的空间先验知识，且由于要对全局建模，导致其计算复杂度为二次方，带来了巨大的计算负担，限制了ViT的适用性。

回顾ViT示意图如下：

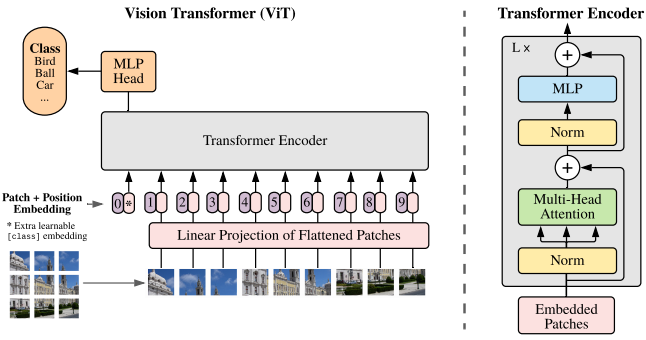
ViT主要可以分成以下步骤：

1、patch embedding：例如输入图片大小为224x224，将图片分为固定大小的patch，patch大小为16x16，则每张图像会生成224x224/16x16=196个patch，即输入序列长度为196，每个patch维度16x16x3=768，线性投射层的维度为768xN (N=768)，因此输入通过线性投射层之后的维度依然为196x768，即一共有196个token，每个token的维度是768。这里还需要加上一个特殊字符cls，因此最终的维度是197x768。

2、positional encoding：ViT同样需要加入位置编码，位置编码可以理解为一张表，表一共有N行，N的大小和输入序列长度相同，每一行代表一个向量，向量的维度和输入序列embedding的维度相同。位置编码的操作是sum，而不是concat。加入位置编码信息之后，维度依然是197x768。

3、LN/multi-head attention/LN：LN输出维度依然是197x768。多头自注意力时，先将输入映射到q，k，v，如果只有一个头，qkv的维度都是197x768，如果有12个头（768/12=64），则qkv的维度是197x64，一共有12组qkv，最后再将12组qkv的输出拼接起来，输出维度是197x768，然后在过一层LN，维度依然是197x768。

4、MLP：将维度放大再缩小回去，197x768放大为197x3072，再缩小变为197x768。

1.2 本文工作

受到RetNet利用一个依赖于距离的时间衰减矩阵为一位和单向文本数据提供显式的时间先验，本文将时间衰减矩阵扩展到空间域，开发了一个基于tokens间曼哈顿距离的二维双向空间衰减矩阵，命名为曼哈顿自注意力MaSA。该注意力允许token感知全局信息，同时为token分配不同级别的注意力。不同的注意力示意图如下：

为了处理自注意因为全局建模带来的巨大计算负担，提出了一种沿图像两个轴分解注意力的方法，在不丢失先验信息的情况下，对自注意力合空间衰减举证进行分解。分解后的MaSA模型具有线性复杂度的全局信息。

2. 方法

回顾retention中的注意力机制：

1）对循环推理表示公式为：

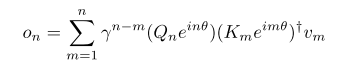
2）对并行训练表示公式为：

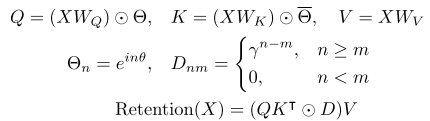
2.1 曼哈顿自注意力

一、从单向衰减到双向衰减

从RetNet中的retention开始，将其演化为MaSA。在MaSA中，将单向和一维的时间衰减转换为双向和二维空间衰减，空间衰减将与曼哈顿距离相关的显式空间先验引入视觉主干，得到等式：

\begin{aligned} BiRetention(X)&=(QK^T\odot D^{Bi})V\\ D^{Bi}_{nm}&=\gamma^{|n-m|} \end{aligned}

其中BiRetention表示双向建模。

二、从一维衰减到二维衰减

虽然现在支持了双向建模，这种能力还局限在一维级别。为了解决这一限制，对一位的Retention进行扩展，在图像的平面中，以二维坐标进行唯一定位，对第n个标记表示为(x_n,y_n)。基于这个修改，调整举证D中的每个元素，以基于它们的2D坐标来表示token之间的曼哈顿距离。矩阵D的重新定义如下：

D_{nm}^{2d}=\gamma^{|x_n-x_m|+|y_n-y_m|}

另外，不同于Retention原文中的将Softmax替换为门控函数，通过实验，在视觉模型中，这种修改并不能改善模型的结果，相反的，它引入了额外的参数和计算复杂度，因此本文继续使用Softmax函数。

结合上述步骤，Manhattan SelfAttention可表示为：

\begin{aligned} MaSA(X)&=(Softmax(QK^T)\odot D^{2d})V\\ D^{nm}_{2d}&=\gamma^{|x_n-x_m|+|y_n-y_m|} \end{aligned}

三、分解曼哈顿自注意力

在ViT 主干的早期阶段，大量的tokens导致在尝试对全局信息进行建模时，自注意力的计算成本巨大。用现有的稀疏注意力或直接使用RetNet的递归/分块递归，会破坏基于曼哈顿距离的控件衰减矩阵，丢失显式空间先验，因此引入一种简单的分解方法如下：

Attn_H=Softmax(Q_HK_H^T)\odot D^H\\ Attn_W=Softmax(Q_WK_W^T)\odot D_W\\ MaSA(X)=Attn_H(Attn_WV)^T\\ D_{nm}^H=\gamma^{|y_n-y_m|},D_{nm}^W=\gamma^{|x_n-x_m|}

具体来说就是分别计算图像水平和垂直反向的注意力分数，然后将一位双向衰减矩阵应用于这些注意力权重。

基于MaSA的分解，每个tokens的感受野形状如下图所示，它于完整的MaSA的感受野形状相同，即完全保留了显式的空间先验知识。

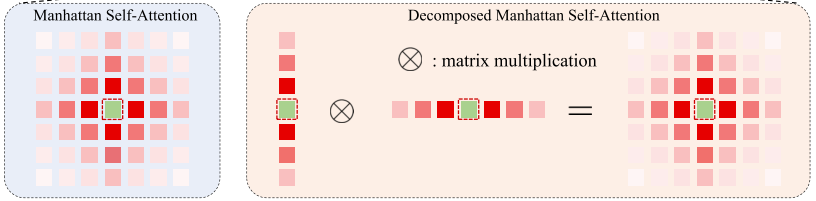
为了进一步增强MaSA的局部表达能力，作者还引入一个局部上下文增强模块，主要又深度可分离卷积构成。

X_{out}=MaSA(X)+LCE（V）

2.2 模型架构

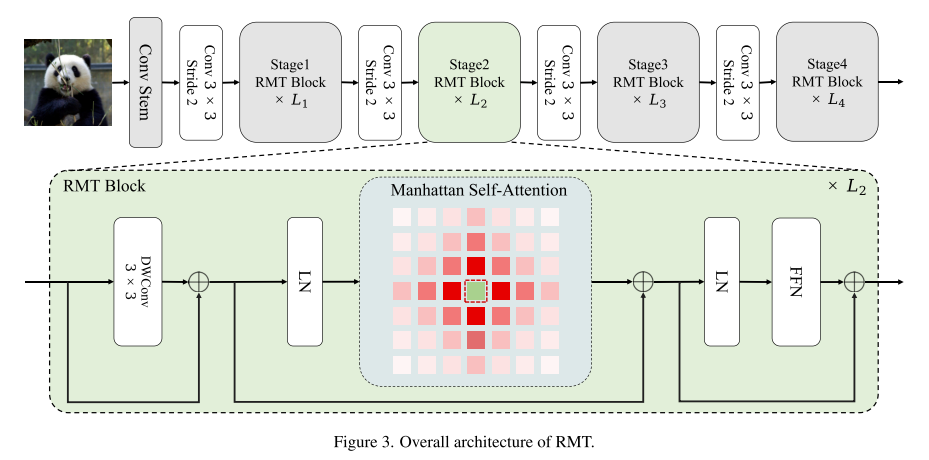
基于MaSA构建了RMT，最终结构如下图所示。RMT分为四个阶段，前三个阶段使用分解的MaSA，而最后一个阶段使用原始MaSA。同时，作者还将条件位置编码（conditional positional encodings，CPE）（为3×3深度卷积）集成到模型中。

本质上可以简单理解为，F 函数是一个二维卷积，这里强调是二维卷积，而不是三维卷积，因为首先进行分割，再将分割后的特征进行了扁平化，所以是二维的（如果直接对图片使用卷积，那卷积核应该是三维的）

为什么使用二维卷积就变成了条件位置编码呢？

这是因为，卷积操作大家都能理解，卷积核尺寸越大（例如 3*3），则包含的周边信息越多，则可以理解为，将原图像的顺序排列的特征具有了空间信息，因此信息包含更多，则能很好的提高准确率。

论文汇报2:Higher-Orde...
论文汇报0：Retentive N...

Comment